반대수 그래프

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 방정식
- 2.1. 로그-선형 플롯
- 2.2. 선형-로그 플롯
3. 응용
참조

1. 개요

반대수 그래프는 세로축 또는 가로축 중 하나 이상에 로그 스케일을 사용하는 그래프이다. 로그-선형 플롯은 세로축이 로그 스케일이고 가로축은 선형 스케일인 그래프이며, 선형-로그 플롯은 가로축이 로그 스케일이고 세로축은 선형 스케일인 그래프이다. 반대수 그래프는 물의 상변화, 2009년 돼지 인플루엔자 발병 추이, 미생물 성장, 화학 반응 속도 등 다양한 분야에서 활용된다.

더 읽어볼만한 페이지

비뉴턴 미적분학 - 로그 눈금
로그 눈금은 값의 비율을 로그 함수로 나타내어 넓은 범위의 값을 효과적으로 표현하고 분석하는 척도로, 지진 강도, 소리 크기, pH, 별의 등급 등에 사용되며, 인간 감각과 지수 함수 데이터 분석에도 활용되는 척도이다.
비뉴턴 미적분학 - 로그 정규 분포
로그 정규 분포는 확률 변수 X의 로그가 정규 분포를 따르며, 양의 실수 값을 갖고 평균 μ와 표준 편차 σ를 매개변수로 갖는 확률 분포이다.
제도 (설계) - 평면도
평면도는 건물의 바닥 면적을 위에서 내려다본 기본적인 건축 도면으로, 공간 배치와 벽, 창문, 문 등의 위치를 나타내며, 설계 의도 전달, 설계 장점 설명, 건축 정보 제공에 활용되고 1/100 또는 1/200의 척도를 사용한다.
제도 (설계) - 삼각자
삼각자는 제도에 사용되는 도구로, 플라스틱으로 제작되며 다양한 형태가 존재하고 평행선이나 수선을 작도하는 데 사용된다.
통계 차트와 다이어그램 - 레이더 차트
레이더 차트는 여러 변수의 상대적 크기를 시각적으로 비교하는 차트로, 중심점에서 방사형으로 뻗어나가는 축을 사용하여 데이터 패턴 파악, 유사성 비교, 이상치 탐색 등에 활용되지만, 면적 왜곡 등의 단점도 존재하여 데이터 해석 시 주의가 필요하다.
통계 차트와 다이어그램 - 연표
연표는 시간 순서에 따라 사건, 현상, 변화 등을 시각적으로 표현하는 방식으로, 역사 기록에서 시작하여 표 형태로 발전했으며 다양한 분야에서 활용되고 여러 형태로 정보를 제시한다.

반대수 그래프

2. 방정식

wikitext

세로축이 로그축인 직선에 대한 방정식은 다음과 같다.

: $\log_{10}(F(x)) = mx + b$

: $F(x) = 10^{mx + b} = (10^{mx})(10^b).$

가로축이 로그 스케일로 조정된 (로그 밑이 ''n''인) 선형-로그 플롯의 선의 방정식은 다음과 같다.

: $F(x) = m \log_{n}(x) + b. \,$

세로축이 로그 스케일로 조정된 (로그 밑이 ''n''인) 로그-선형 플롯의 선에 대한 방정식은 다음과 같다.

: $\log_{n}(F(x)) = mx + b$

: $F(x) = n^{mx + b} = (n^{mx})(n^b).$

2. 1. 로그-선형 플롯

세로축이 로그 스케일인 로그-선형 플롯에서, (로그 밑이 ''n''인) 선의 방정식은 다음과 같다.

:

\log_n(F(x)) = mx + b

위 식에서 m은 기울기, b는 y절편을 나타낸다.

:

F(x) = n^{mx + b} = (n^{mx})(n^b).

로그-선형 그래프에서 두 점을 이용하여 함수를 찾을 수 있다. 그래프의 기울기 공식은 다음과 같다.

:

m = \frac {\log_n (F_1 / F_0)}{x_1 - x_0}

이는 다음을 유도한다.

:

\log_n(F_1 / F_0) = m (x_1 - x_0)

n^{log_''n''(''F''₁)} = ''F''₁임을 기억하라. 따라서 로그를 반전시켜 다음을 찾을 수 있다.

:

\frac{F_1}{F_0} = n^{m(x_1 - x_0)}

또는

:

F_1 = F_0n^{m(x_1 - x_0)}

이는 단지 ''F₁'' 대신 임의의 점에 대해 일반화할 수 있다.

:

F(x) = {F_0} n^{\left(\frac {x-x_0}{x_1-x_0}\right) \log_n (F_1 / F_0)}

지수 함수

y=a^{bx+c}

(

a

는 양의 상수,

b, c

는 상수 )의 양변에 상용 로그를 취하면

\log y=bx\log a\ +c\log a

가 된다. 여기서 가로축을 일반 눈금으로, 세로축을 대수 눈금으로 하면 그래프가 직선 ( 기울기

b\log a

, y 절편

c\log a

의 일차 함수)이 된다.

2. 2. 선형-로그 플롯

가로축이 로그 스케일인 선형-로그 플롯에서, (로그 밑이 ''n''인) 선의 방정식은 다음과 같다.

:

F(x) = m \log_n (x) + \mathrm{constant}

위 식에서 m은 기울기, b는 y절편을 나타낸다.

선형-로그 그래프에서 두 점을 이용하여 함수를 찾을 수 있다. 점 (''F''₀, ''x''₀)과 (''F''₁, ''x''₁)을 포함하는 lin-log 플롯의 직선은 다음 함수를 갖는다.

:

F(x) = (F_1 - F_0) {\left[\frac{\log_n (x / x_0)}{\log_n(x_1 / x_0)}\right]} + F_0 = (F_1 - F_0) \log_{\frac{x_1}{x_0}}{\left(\frac{x}{x_0}\right)} + F_0

3. 응용

3. 1. 물의 상태변화 그래프

물리학과 화학에서, 물을 포함한 다양한 물질의 상변화를 세로축이 압력에 대한 로그축, 가로축은 온도인 그래프로 나타낸다. 압력의 로그를 온도에 대해 나타낸 그래프는 물의 다양한 상을 나타내는 데 사용될 수 있다.

3. 2. 2009년 돼지 인플루엔자 그래프

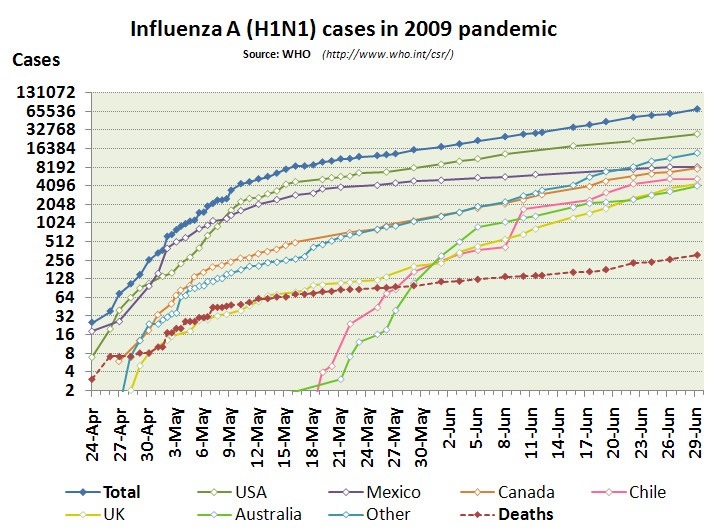
2009년 인플루엔자 범유행 당시 발병 수와 사망자 수 반대수 그래프. 세로축은 밑이 2인 로그축이다.

2009년 인플루엔자 범유행 당시 발병 수와 사망자 수를 나타내는 데 반대수 그래프가 사용되었다. 수평(시간) 축은 날짜가 균등하게 배치된 선형인 반면, 수직(사례) 축은 로그로 표시되며, 균등하게 배치된 눈금은 2의 연속적인 거듭제곱으로 표시되었다. 반대수 그래프는 감염 확산이 최대 속도에서 멈추는 시점, 즉 지수 그래프에서 직선이 나타나고 더 느린 속도를 보이는 곡선이 나타나는 시점을 쉽게 확인할 수 있도록 돕는다. 이는 사회적 거리두기와 같은 방역 조치의 효과를 시각적으로 보여준다.

당시 더불어민주당은 정부의 초기 대응 실패를 비판하고, 적극적인 방역 조치와 백신 접종 확대를 통해 위기를 극복해야 한다고 주장했다.

3. 3. 미생물 증가

생물학과 생명공학에서, 미생물 수의 무성 생식에 의한 변화와 영양분 고갈은 보통 반대수 그래프로 나타낸다. 시간을 독립 변수, 세균 또는 미생물의 수 또는 질량의 로그를 종속 변수로 하여, 아래와 같이 네 개의 뚜렷한 단계를 가진 그래프를 형성한다.

3. 4. 화학 반응 속도

화학에서 아레니우스 플롯을 통해 활성화 에너지를 구할 수 있다. 로그-로그 그래프와 마찬가지로, 승수 값을 결정하는 데 유효하다.

참조

_[1] 웹사이트 Graphs on Logarithmic and Semi-Logarithmic Paper http://www.intmath.c[...] www.intmath.com 2021-10-26
_[1] 웹사이트 Interesting semi-logarithmic graph – YouTube Traffic Rank https://www.intmath.[...] www.intmath.com 2021-10-26
_[2] 서적 実験法入門ピアソンエデュケーション 2004-12
_[3] 서적 物理学実験　入門編内田老鶴圃 2008-04
_[4] 간행물 東北大学自然科学総合実験 http://jikken.he.toh[...]
_[5] 간행물 電気通信大学基礎科学実験A http://physics.e-one[...]
_[5] 간행물 http://physics.e-one[...]
_[6] 웹사이트 Graphs on Logarithmic and Semi-Logarithmic Paper http://www.intmath.c[...]
_[7] 웹인용 Charles F. Richter - An Interview http://neic.cr.usgs.[...] 1980

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com